描述统计
描述统计(Descriptive Statistics)是定量地描述或总结样本中变量特征的统计方法。
分析资料时,首先要用适当的描述统计方法来简化资料中的各个变量,然后进一步分析变量之间的关系。
按照变量的数量,描述统计可以分为:单变量描述统计、双变量描述统计、多变量描述统计。
单变量描述统计
单变量描述统计分析按照变量的测量层次,可以分为无序类别变量的描述统计分析、有序类别变量的描述统计分析以及数值变量的描述统计分析。
单变量描述统计的维度有:
- 集中趋势。如众数、平均值、中位数等。
- 离散特征。如异质指数、四分位差、方差、标准差。
- 分布特征。如偏度、峰度。
无序类别变量的描述统计
适用于无序类别变量的描述统计方法,有次数分布、比例、比率、图示和对比值等。
次数分布
次数分布(frequency distribution),就是变量中每一个值的出现次数。通过次数分布,可以看出变量中不同取值的多少。不同规模样本中的次数分布不能直接比较。
比例
比例(proporitions) 就是将每个类别的次数 \(f\) 除以总数\(N\)。公式为:\(P = \dfrac{f}{N}\)。通过计算比例,可使不同样本规模的总数成为同一个基数,即都是1。
比率
比率(rates)就是把比例的基数变大,使读者更容易领会。社会科学中最常用的比率是百分率(%),在汇报结果时,通常保留1到2位小数。
众值
适合无序类别变量的集中趋势指标是众值(mode)。众值就是出现次数最多的值。使用众值预测所犯的错误总数是最少的。
类别数据可视化
在社会科学中多使用柱状图和饼图描述无序类别变量。
有序类别变量的描述统计
适用于无序类别变量的描述统计方法,如次数分布、比例、比率、柱状图、饼图,也适用于有序类别变量。还有针对有序类别变量的描述统计方法:累计次数、累加百分率。
累加次数
累加次数(cumlulative frequencies),简写cf,就是把次数逐级相加起来。分为两种,一种是向上累加,一种是向下累加。累加次数的作用是使我们容易知道某值以下或者以上的次数总和。
累加百分比
累加百分比(cumulative percentages),简写c%,就是将各级的百分率数值逐级相加。
数值变量的描述统计
使用均值、中位数、众数描述集中趋势:
- 均值(Mean):所有数值的总和除以数值的个数。它提供了数据集的平均水平。
- 中位数(Median):将数据集从小到大排列后位于中间位置的数值。对于偏态分布的数据,中位数是一个更好的中心趋势度量。
- 众数(Mode):数据集中出现次数最多的数值。对于分类数据和离散数据非常有用。
使用范围、四分位数、标准差、方差描述离散趋势:
- 范围(Range):最大值和最小值之间的差异。
- 四分位数范围(Interquartile Range, IQR):第25百分位数(Q1)和第75百分位数(Q3)之间的差,用于衡量中间50%数据的离散程度。
- 标准差(Standard Deviation):度量数据点与均值的平均距离。
- 方差(Variance):标准差的平方,表示数据的总体变异性。
使用偏度、峰度描述分布形状:
- 偏度(Skewness):度量数据分布的不对称性。正偏度表示数据向右偏斜,负偏度表示向左偏斜。
- 峰度(Kurtosis):描述数据分布的尖锐程度。高峰度表示数据分布比正态分布更尖锐。
使用直方图、箱型图进行可视化描述:
- 直方图(Histogram):展示数据的频率分布。
- 箱形图(Box Plot):展示数据的中位数、四分位数以及异常值。
双变量描述统计
双变量的描述统计,可以使用诸如交叉表、散点图的图表及相关系数等方式对两个变量之间的相关性进行统计。
相关性
所谓相关性,是指一个变量的变化与另一个变量的变化有连带性。
如教育水平和人生志愿、性别和内容消费行为的偏好等等。
相关的强度与方向
大多数的统计方法是以 0 代表无相关,以 1 代表完全相关。不同测量层次有着不同的相关系数。
| 相关系数 | 关联程度 |
|---|---|
| 0.19 以下 | 微弱相关或无相关 |
| [0.29-0.39] | 弱相关 |
| [0.40-0.59] | 中度相关 |
| [0.60-0.79] | 强相关 |
| [0.80-1.0) | 非常强 |
| 1 | 完全相关 |
相关还有方向的区分,如正相关表示一个变量增加时,另外一个变量也在增加。
不对称关系与对称关系
\(X\)影响\(Y\),但是\(Y\)不影响\(X\),这种情况称之为不对称关系,反之,为对称关系。
因果关系
相关的两个变量,不一定有因果关系,可能是共同变化。
在研究中,会假定某变量是因,称为自变量(independent variable),另一个变量为结果,称为因变量(dependent variable)。
保罗·拉扎斯菲尔德提出了两个变量存在因果关系的三个条件:
- 原因出现在结果之前;
- 变量之间存在相关关系;
- 两个变量之间的相关性不能被与这两个变量都相关的第三个或更多变量所解释。
还有学者提出如下条件:
- 存在事件的时间顺序,原因事件在结果事件之前。这称之为时间优先(temporal precedence)。
- 原因事件呈现时,结果事件发生。原因事件不呈现时,结果事件不发生。这称之为原因与结果的协变化(covariation of cause and effect)。
- 除了原因变量外,没有其他因素能够是观察到的结果的原因。这称之为排除备择解释(alternative explanations)。
消除误差比例
PRE 是 Proportional Reduction in Error(消除误差比例)的缩写,这是一个在统计学中常用来衡量模型或预测方法有效性的指标。PRE 主要用于评估一个预测模型或方法相比于简单的基准模型在减少预测误差方面的改进程度。它是一个相对度量,通常以百分比表示,
公式为:\[PRE=\dfrac{E_1-E_2}{E_1}\]
\(E_1\)表示不知道\(X\)的值,预测\(Y\)值时所产的全部误差。\(E_2\)表示知道\(X\)的值,预测\(Y\)值时所产生的全部误差。
假设一名教师,想要预测班上学生的数学考试成绩,有两个模型:一个是基准模型,另一个是更复杂的模型。
- 基准模型:预测每个学生的成绩都是班级平均成绩。假设班级平均成绩是 70 分。 假设总误差(所有学生的实际成绩与平均成绩差异的总和)是 800 分。
- 复杂模型:可能基于学生的历史成绩、出勤率等因素来预测他们的考试成绩。假设使用这个模型后,总误差降低到 500 分。
现在,我们要计算 PRE,即复杂模型相比基准模型在减少预测误差方面的改进程度。
- 基准模型的总误差:800 分。
- 复杂模型的总误差:500 分。
- 计算 PRE:
- \(PRE = \dfrac{(基准模型的总误差 - 复杂模型的总误差)}{基准模型的总误差}\)
- \(PRE = \dfrac{(800 - 500)}{800} = \dfrac{300}{800} = 0.375\)
这个 PRE 值 0.375 表示复杂模型在减少预测误差方面比基准模型有 37.5% 的改进。换句话说,相比于简单地使用班级平均成绩作为每个学生的预测成绩,复杂模型减少了约 37.5% 的预测误差。
通过这个例子,可以看到 PRE 是如何帮助我们量化和评估一个预测模型的有效性的。这个指标特别有用,因为它提供了一个直观的方式来比较不同模型对于减少预测误差的能力。
社会科学选择相关系数的三个标准
- 两个变量的测量层次。
- 两个变量的关系是否对称。
- 优先选择具有消除误差比例意义的统计值。
两个无序类别变量相关性描述统计
两个无序类别变量之间的相关测量,可以使用Lambda相关测量、古德曼和古鲁斯卡的tau-y相关测量。除了上述的两种系数外,还有phi相关系数、列联相关系数、V相关系数等,但这些系数都不具有消除误差比例的意义。
Lambda相关测量法
Lambda相关测量法有两种形式,一种是对称的,简写为\(\lambda\)系数,一种是不对称的,简写为\(\lambda_y\)系数。Lambda系数是以众值作为预测的准则,如果全部众值集中在条件次数表的同一行或同一侧,则Lambda系数便会等于0。因此,Lambda相关测量法存在敏感性问题。\(\lambda_y\)系数具有消除误差比例的意义。
古德曼和古鲁斯卡的tau-y系数
tau-y系数是属于不对称相关测量法,要求两个变量一个是因变量,另一个是自变量。tau-y系数具有消除误差比例的意义。tau-y系数用到了全部边缘次数和条件次数,故其敏感度高于Lambda测量法,如果是不对称关系,应优先选用tau-y系数。
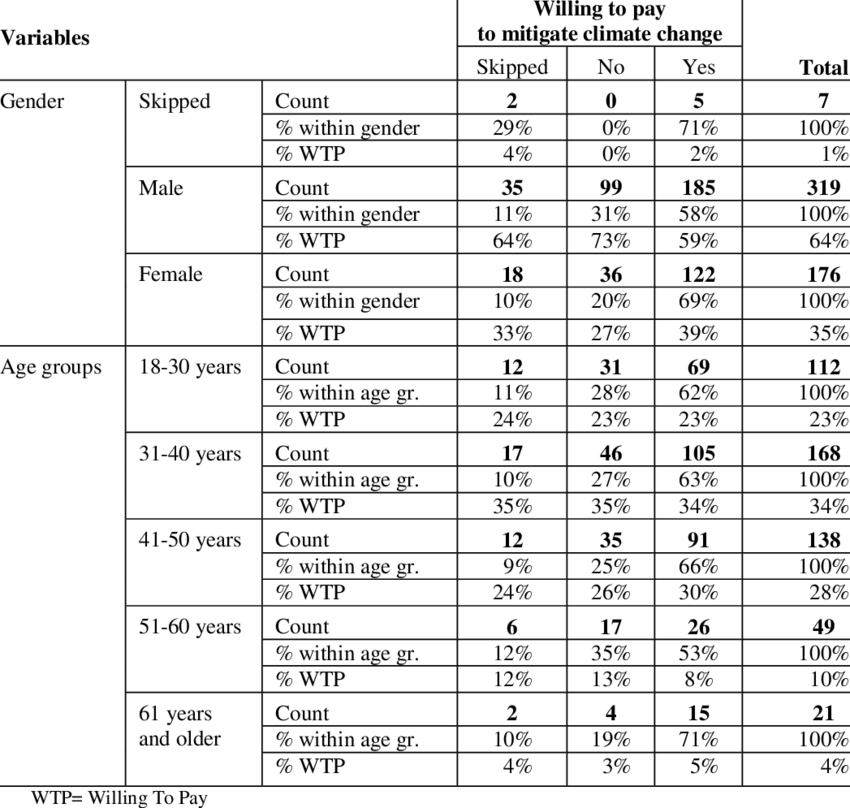
交互分类表
交互分类(cross classification)是最基本的两个变量相关情况的描述统计方法。交互分类表又称为条件次数表,在表中的总次数称之为边缘次数,表中的其他次数称为条件次数。按照百分比计算的条件次数表称为条件百分表。
交互分类就像是我们把事物根据两种不同的特征进行分类。举个例子,如果我们有一群人,我们可以根据他们的性别(男或女)和年龄(比如青年、中年、老年)来对他们进行分类。这样做的目的是为了查看不同组合(比如年轻女性或中年男性)的人在某些方面(如喜好、行为等)是否有明显的不同,从而帮助我们理解这些特征之间是否存在某种联系。
当我们使用两个变量来分类时,比如性别和年龄,我们所创建的表格被称为“两维列联表”。如果我们加入第三个变量,比如职业,那么这个表格就变成了“三维列联表”。类似地,如果有更多的变量,就会产生所谓的“多维列联表”或“高维列联表”。而如果我们只根据一个变量来分类,比如只看性别,那么这样的表格就是简单的“频数分布表”,它告诉我们每个类别(如男性或女性)的人数。
在社会科学研究中,通常将自变量作为计算百分率的方向,即将自变量放置在条件百分表的列中。但如果因变量在样本中的分布不能代表其在总体内的分布,则以因变量为计算百分率的方向。
无序类别变量相关性的可视化
- 条形图:对每个类别组合绘制一个条形,展示频数或比例。条形图直观、易于理解,适合比较不同组合之间的差异。
- 堆叠条形图:在单个条形中展示每个子类别的比例,有助于比较不同类别组合内部的构成。
- 热力图:使用颜色深浅表示频率或数量,适合展示大量数据,能够清楚地显示不同类别组合之间的关系强度。
- 马赛克图:通过不同大小的矩形展示频率或比例,每个矩形的面积对应于相应类别组合的数据大小。
两个有序类别变量相关性描述统计
两个有序类别变量,除了采用两个无序类别变量的相关测量法之外,还可以使用Gamma系数和Somers的dy系数等级序相关测量法(rank-order correlation methods)。
Gamma系数
Gamma系数适合于对称关系。该系数具有消除误差比例的意义。\(G = \dfrac{N_s-N_d}{N_s+N_d},其中\)\(N_s\)是同序对数。某对个案在两个变量上的相对等级是相同的。\(N_d\)是异序对数。某对个案在两个变量上的相对等级是不同的。
Somers dy系数
\[d_y = \dfrac{N_s-N_d}{N_s+N_d+T_y}\]
- \(N_s\)是同序对数。某对个案在两个变量上的相对等级是相同的。
- \(N_d\)是异序对数。某对个案在两个变量上的相对等级是不同的。
- \(T_y\)是只在因变量Y上同分的对数。
该系数适用于非对称关系,且具有消除误差比例的意义。
肯德尔的tau系数
该系数有3种形式,肯德尔的 Tau-a 和 Tau-b 是两种用于衡量两个有序变量之间相关性强度的非参数统计方法。Tau-a 适用于任意大小的样本和列联表,但更常用于小样本情况。Tau-b 适用于方形或非方形的列联表,特别是样本量较大时。Tau-c 特别适用于方形的列联表,即行和列的数量相等的情况。
该系列参数不具有消除误差比例意义。
斯皮尔曼秩相关系数
斯皮尔曼秩相关系数(Spearman’s rank correlation coefficient),通常表示为 \(r_s\),是一种非参数的统计度量,用于评估两个变量之间的相关性,特别是它们的单调关系。这种相关系数不需要数据符合正态分布,适用于顺序变量(即有序分类变量)和连续变量。
斯皮尔曼秩相关系数主要用于衡量两个变量之间的单调关联程度,它反映的是变量间的相对位置变化的一致性,而不是误差的减少。
斯皮尔曼秩相关系数的计算步骤如下:
将每个变量的数据转换为秩次。即,数据集中的每个值被替换为它在数据集中的排序位置。
计算两个变量的秩次之差以及差值的平方。
应用下列公式计算斯皮尔曼秩相关系数: \[r_s = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)}\]
其中,\(d_i\) 是两个秩次之差,\(n\) 是数据点的数量。
无序类别变量相关性可视化
两个有序类别变量相关性可使用交互分类表进行展示,还可通过散点图、条形图、热力图等图形进行相互关系的可视化。
两个数值变量相关性描述统计
两个变量都是数值变量,则可以用简单回归分析法以自变量的值预计因变量的数值,用积矩相关系数来测量两个变量的相关强度和方向。
简单线性回归分析
回归分析的目的,是要找出一个错误最小的方法来预测因变量的数值。回归方法中最容易的是简单线性回归分析法,它根据方程\(Y=bX+a\)来预测。\(b\)称为回归系数,表示直线的斜率。如果以一条简单的直线作为预测的工具,则上述方程所犯的误差总数是最小的。
回归系数\(b\)是分析不对称关系的统计法,但是其值不一定在-1和+1之间,它的大小是随变量的衡量单位而定,没有一定的范围,故很少用\(b\)来表示相关程度的强弱。
积矩相关测量法
皮尔逊积矩相关系数(Pearson’s product-moment correlation coefficient),通常简称为皮尔逊相关系数,是统计学中用于度量两个变量之间线性相关程度的一个指标,适用于连续变量且假定这些变量至少近似服从正态分布。该系数由卡尔·皮尔逊(Karl Pearson)提出,是最常用的相关系数之一。
皮尔逊积矩相关系数 \(r\) 的计算公式为:
\[ r = \frac{\sum (X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum (X_i - \bar{X})^2 \sum (Y_i - \bar{Y})^2}}\]
其中,\(X_i\) 和 \(Y_i\) 是两个变量的观测值,\(\bar{X}\) 和 \(\bar{Y}\) 是各自的平均值。
皮尔逊积矩相关系数\(r\),用于分析对称关系,其值在-1和+1之间,同时\(r^2\)具有消除误差比例的意义。\(r^2\) 称为决定系数。\(r\) 系数所表示的,就是以线性回归方程式作为预测的工具时所能减少的误差比例。因此,如果\(r\)系数值越大,一方面表示线性回归方程式的预测能力越强,另一方面也表示两个变量之间的关系越接近于线性关系。
皮尔逊积矩相关系数对异常值敏感,异常值可能显著影响相关系数的大小。另外仅限于线性关系,如果两个变量之间的关系是非线性的,即使它们非常密切,皮尔逊积矩相关系数也可能接近于零。
确定两个数值变量之间是否线性相关
两个数值变量的相关性,可通过散点图进行观察,如果发现散点图中的分布显然不是直线形状,就不能用\(r\)系数来测量相关情况。测量非线性相关的方法有很多,其中的一种就是相关比率。
除了使用散点图直接观察外,还可将相关比率的开方(E值)与积矩相关系数r值进行比较,可以大致上判断是否非直线关系。两值相差越大,显示两个数值变量之间的关系越是非线性。
数值变量相关性可视化
两个数值变量之间的相关性可以通过多种方式可视化。最常用的方法包括:
- 散点图(Scatter Plot):这是最直观的方法,可以清楚地展示两个变量的相关性。如果两个变量正相关,散点图上的点会呈现向上的趋势;如果负相关,则呈现向下的趋势;如果不相关,则点呈分散分布。
- 线性回归图(Linear Regression Plot):这是在散点图的基础上添加一条最佳拟合线,可以更清楚地展示变量间的线性关系。
- 热力图(Heatmap):当需要同时展示多个变量之间的相关性时,热力图是个好选择。热力图可以通过颜色的深浅来展示相关系数的大小,非常适合于展示相关系数矩阵。
- 等高线图(Contour Plot):这种图用等高线展示两个变量的密度,可以帮助识别变量间的关系模式,尤其是在数据点非常密集的情况下。
无序类别变量与数值变量相关性描述统计
当以无序类别变量为自变量,以数值变量为因变量时,可采用相关比率作为相关测量方法。
相关比率
相关比率(correlation ratio),由俄罗斯数学家和统计学家安德烈·马尔科夫(Andrey Markov)提出,又称为eta系数\(\eta\)。\(\eta^2\)的值介于0到1之间,具有消除误差比例的意义。相关比率除了分析无序类别变量与数值变量的相关之外,还可以分析两个定距变量之间的非线性关系。
相关比(correlation ratio)具体的计算公式如下:
设 \(Y\) 是数值变量,\(X\) 是分类变量,\(X\) 有 \(k\) 个类别。对于每个类别 \(i\),计算其内的数值变量 \(Y\) 的均值\(\bar{Y}_i\) 和样本数 \(n_i\)。设 \(Y\) 的总均值为\(\bar{Y}\)。
- 组内平均方差(Within-group Variance): \[ \text{Variance}_{\text{within}} = \sum_{i=1}^{k} \frac{1}{n_i} \sum_{j=1}^{n_i} (Y_{ij} - \bar{Y}_i)^2 \] 这里,\(Y_{ij}\) 是第 \(i\) 组中的第 \(j\) 个观察值。
- 总方差(Total Variance): \[ \text{Variance}_{\text{total}} = \sum_{i=1}^{k} \sum_{j=1}^{n_i} (Y_{ij} - \bar{Y})^2 \]
- 相关比(Correlation Ratio): \[ \eta = \sqrt{1 - \frac{\text{Variance}_{\text{within}}}{\text{Variance}_{\text{total}}}} \]
类别变量与数值变量相关性的可视化
类别变量与数值变量之间的相关性可视化通常会采用以下几种方法:
- 箱形图(Boxplot):箱形图非常适合展示一个类别变量与一个数值变量之间的关系。每个类别的数据都以一个箱子的形式展示,其中包含中位数、四分位数等统计信息。箱形图可以很好地展示不同类别在数值变量上的分布差异。
- 小提琴图(Violin Plot):小提琴图是箱形图的一种变体,它在展示类别数据的中位数和四分位数的同时,还展示了数据分布的密度估计。这使得小提琴图能提供比箱形图更丰富的信息。
- 条形图(Bar Plot):如果你想要展示每个类别在数值变量上的平均值或总和,条形图是一个很好的选择。它可以直观地展示不同类别在某个数值指标上的比较。
- 点图(Point Plot):点图类似于条形图,但它通过点和线来表示数值,而不是条形。点图适合于展示类别间的数值差异以及趋势。
- 蜂群图(Bee Swarm Plot):蜂群图是另一种展示类别数据分布的方法,它可以避免箱形图或小提琴图中的重叠问题,更好地展示数据的分布情况。
无序类别变量与有序类别变量相关性描述统计
将有序类别变量降低到无序类别变量,然后按照两个无序类别变量进行统计分析。
有序类别变量与数值变量相关性描述统计
将有序类别变量降维到无序类别变量,然后使用无序类别变量与数值变量的分析方法进行处理。
多变量描述统计
多变量描述统计在许多领域中都非常重要,如市场研究、社会科学、生物统计学、环境科学等。它帮助研究人员和决策者理解数据的多维特性,揭示变量间的复杂关系。多变量描述统计关注的是变量之间的关系和相互作用。
使用统计方法来分析多个变量之间的复杂关系。这可能包括因子分析、主成分分析、聚类分析等。还可绘制平行坐标图、雷达图等,展示多个变量间的关系。
类别变量最常见的多变量描述统计,可以使用多维交互分类表进行。
在进行多变量描述统计时,多数时候,需要和推论统计相结合。
参考文献
- 李沛良. (2001). 社会研究的统计应用. 社会科学文献出版社.
- matplotlib.pyplot — Matplotlib 3.5.2 documentation
- matplotlib.axes.Axes.pie — Matplotlib 3.5.2 documentation
- Categorical data — pandas 1.4.3 documentation (pydata.org)
- Somers’ D - HandWiki
- scipy.stats.somersd — SciPy v1.9.0 Manual
- Gamma Coefficient (Goodman and Kruskal’s Gamma) & Yule’s Q (statisticshowto.com)
- Somers’ d using SPSS Statistics | A How-To Statistical Guide by Laerd Statistics
- scipy.stats.pearsonr — SciPy v1.9.0 Manual