推论统计

对样本资料进行描述统计后，我们还要根据样本的研究结果来推测总体的情况。以样本的数值来推算总体，结论可能正确，也可能错误，而运用概率论原理，我们可以求出推论统计犯错的可能性大小。只要我们是采用随机抽样方法，就可以根据抽样分布，以样本的数值来推测总体的情况。

推论统计一般分为两大类：参数估计（parameter estimation）和假设检验（hypothesis testing）。参数估计是根据随机样本的统计值来估计总体的参数值。假设检验是先提出假设总体的情况，再以随机样本的统计值来检验这个假设是否正确。社会研究大多数采用假设检验的推论统计分析方法。

参数估计

参数估计是推论统计学中的一个核心概念，旨在根据样本数据估计总体的未知参数。这里的参数通常是指总体的某些特征，如均值、方差、比例等。参数估计主要分为两类：点估计和区间估计。

点值估计

设总体\(X\)的分布函数的形式已知，但它的一个或多个参数未知，借助于总体\(X\)的一个样本来估计总体未知参数的值的问题称为参数的点估计问题。

点值估计，就是以一个适当的样本统计值来代表总体的参数值。如用样本均值\(X\)估计总体均值\(\mu\)，或者用样本标准差\(S\)估计总体标准差\(\sigma\)。

例如：

报告显示，截至2022年6月，我国网民规模为10.51亿，较2021年12月新增网民1919万，互联网普及率达74.4%。网民人均每周上网时长为29.5个小时，使用手机上网的比例达99.6%。

但是点估计不能提供估计参数的估计误差大小，所以点估计主要为许多定性研究提供一定的参考数据，或在对总体参数要求不精确时使用，而在需要用精确总体参数的数据进行决策时则很少使用。

区间估计

区间估计指的是，在点估计的基础上，以区间的形式估计出一个范围，并给出这个范围中包含参数值真值的可信程度。区间估计就是以两个数值之间的间距来估计参数值，至于间距的大小，取决于可信程度（也叫置信度）。间距的大小（误差范围）与置信度（可靠程度）的高低成反比。

均值的区间估计

\[\bar{X}\pm1.96(\frac{S}{\sqrt{n}})\]

其中1.96为95%置信水平对于的\(Z\)值。\(S\)为样本标准差，\(n\)是样本规模，\(\bar{X}\)是样本的平均值。

比例值的区间估计

\[p\pm1.96\sqrt{\frac{p(1-p)}{n}}\]

其中\(p\)为样本的比例值，\(n\)为样本规模，1.96为95%置信水平对于的\(Z\)值。

假设检验

假设检验是推论统计中除参数估计参数估计之外的另一种类型。在总体未知的情况下，为了推断总体的某些特征，提出关于总体的假设，根据样本对所提出的假设做出接受还是拒绝的决策。这个已有的结论或主张在概率的语境中称为“假设” Hypothesis，对应的对这个主张的求证的过程，称为“检验” Test。

研究假设与虚无假设

假设检验的基本过程是首先假设样本某方面的参数是否符合某个假设而建立两个互斥的判断条件：

• 虚无假设 Null hypothesis：\(H_0\)，虚无假设通常表示“没有变化”或“没有效果”的状态。
• 研究假设 Alternative hypothesis：\(H_a\)，备选假设是与虚无假设相对立的假设，通常表示“有变化”或“有效果”。

之后通过从总体中进行抽样，对目标参数进行统计，然后根据样本统计数据来定量的推断总体的参数符合哪一个假设。在实际应用中，将哪个假设设置为虚无假设以及研究假设不一定是一目了然的，需要结合研究的对象具体判断。

更一般地，如果令 \(μ_0\) 来代表事先主张的某个值，根据不同的假设设定，零假设和备选假设共有三种形式：

• \(H_0: μ ≥ μ_0，H_A: μ < μ_0\)
• \(H_0: μ ≤ μ_0，H_A: μ > μ_0\)
• \(H_0: μ = μ_0，H_A: μ ≠ μ_0\)

值得注意的是，三种形式下相等的部分都发生在零假设下，且后续会知道前两种形式称为单侧检验（one-tailed test），最后一种为双侧检验（two-tailed test）。

假设一家广告公司想要测试一种新的在线广告策略是否比现有策略更有效。他们的目标是提高广告点击率（CTR，Click-Through Rate），即观众点击广告的比例。

• 虚无假设（\(H_0\)）：新的广告策略不会改变广告点击率。换句话说，新策略和旧策略的效果是一样的。可以数学化表示为：\(H_0: CTR_{\text{新策略}} = CTR_{\text{旧策略}}\)
• 备选假设（\(H_1\)）：新的广告策略会改变广告点击率。这种改变可以是提高也可以是降低（如果我们只关心提高，备选假设将是单向的）。可以数学化表示为：\(H_1: CTR_{\text{新策略}} \neq CTR_{\text{旧策略}}\)

公司会基于一定数量的样本数据（例如，观察两种策略各自的点击数据）来进行统计检验。如果检验结果表明有足够证据拒绝虚无假设，那么他们可能会决定采用新的广告策略。反之，如果没有足够证据拒绝虚无假设，那么他们可能会保持现有策略不变。

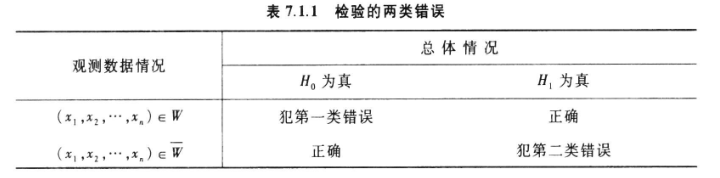
类型 I 与类型 II 错误

理想情况下无论支持或否定零假设都是基于统计事实的正确决策，但实际情况是由于样本选取的不同，或者说由于抽样误差的存在，我们可能在虚无假设本身是正确的情况下选择了拒绝零假设，转而支持研究假设，当然也存在零假设原本应该被拒绝的情况下错误的选择了支持零假设，这两类错误分别称为 Type I 错误和 Type II 错误。I 类错误意味着错误地拒绝零假设。

类型 I 与类型 II错误的概率

由于检验结果受样本的影响，具有随机性，于是，可用总体分布定义犯第一类错误、第二类错误的概率如下：

• 犯第一类错误的概率：\(\alpha(\theta)=P_{\theta}\{\boldsymbol{X} \in W\}, \theta \in \Theta_{0}\)
• 犯第二类错误的概率：\(\beta(\theta)=P_{\theta}\{\boldsymbol{X} \in \bar{W}\}, \theta \in \Theta_{1}\)

类型 I 与类型 II特点

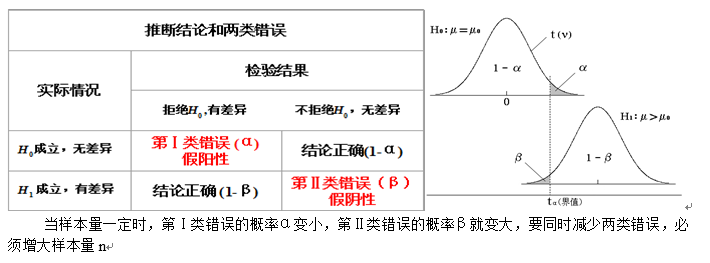
在样本量给定的条件下，第一类错误与第二类错误中一个减少必然会导致另一个增大。不可能找出一个使第一类错误和第二类错误都小的检验。要同时减少两类错误，必须增大样本量\(n\)。

既然我们不能控制同时控制一个检验犯第一类错误α和第二类错误的概率β，但可以限制仅仅犯第一类错误的概率。

统计学中提出显著性检验就是要控制犯第一类错误的概率α，但也不能使得α过小。在适当控制α中制约β。最常用的选择是α=0.05，有时也选择α=0.10或α=0.01。

β与检验功效

在假设检验中，β代表第二类错误（当原假设为假，而我们却接受了原假设）发生的概率。那么，当原假设为假，我们正确拒绝原假设的概率就是1-β，这个值就叫做检验功效（Power）。

显著性水平

显著性水平（Level of Significance）是一种检验标准，用α表示。显著性水平是当虚无假设为真时拒绝虚无假设所犯错误的标准。即估计总体参数落在某一区间内可能犯错误的概率。

\[显著性水平=p(I类错误)=α\]

显著性水平表示当原假设正确时，测试将产生具有统计显著性结果的概率。显著性水平等于类型 I 错误率。因此可以将此错误率视为误报的概率。

显著性水平是由研究者事前确定的，具有一定的主观性。在社会科学中，通常设定为0.05或者0.01.

在确定显著性水平后，就可以定出检验的拒绝域。

显著性检验

显著性检验是统计学中一种用来确定样本结果是否有统计显著性的方法，即判断样本结果是否足以拒绝虚无假设。这种检验的核心在于评估观察到的数据模式是否可能仅仅是由随机变化引起的。

对检验问题\(H_{0}: \theta \in \Theta_{0}\) VS \(H_{1}: \theta \in \Theta_{1}\), 如果一个检验满足对任意\(\theta \in \Theta_{0}\) 都有\(g(\theta) \leqslant \alpha\)则称该检验是显著性水平为α的显著性检验，简称水平为α的检验。

提出显著性检验的概念就是要控制犯I类错误的概率α，但也不能使得α过小（α过小会导致β过大），最常用的选择是α=0．05，有时也选择α=0.01或α=0.001。

p值

在一个假设检验问题中，利用样本观测值能够做出拒绝虚无假设的最小显著性水平称为显著性检验的p值。p值是在原假设为真的情形下，大于检验所得值（可以是Z值、t值、F值或卡方值）的概率。

p 值（p-value，又称概率值或概值）是指假如虚无假设正确的话，进行试验得到现有样本以及比现有样本情况更极端的情形的累计概率。

想象一下，你在玩掷硬币的游戏，怀疑这枚硬币可能是偏重的（不公平的）。为了测试这个想法，你决定进行一个实验：掷这枚硬币多次，然后看看结果。

在这里，你的虚无假设（即默认的假设）是硬币是公平的，也就是说，得到正面或反面的机会各是一半。

假设你掷了硬币100次，结果竟然有70次是正面。这看起来有点不寻常，因为如果硬币是公平的，正面和反面的出现次数应该大致相同。 在这种情况下，p值就是告诉我们，在硬币确实是公平的情况下，出现至少70次正面的概率有多大（计算结果为0.0039%）。如果这个概率非常低（比如小于5%），我们就会怀疑硬币可能真的是偏重的，并考虑拒绝“硬币是公平的”这一虚无假设。

from scipy.stats import binom

# 总共掷硬币的次数
n = 100
# 成功的次数，即出现正面的次数
k = 70
# 单次掷硬币出现正面的概率（公平硬币）
p = 0.5

# 计算至少出现k次正面的概率
# 使用累积分布函数（CDF）计算小于等于69次正面出现的概率，然后用1减去这个概率得到至少出现70次正面的概率
prob_at_least_70 = 1 - binom.cdf(k-1, n, p)
prob_at_least_70
3.925069822796612e-05

p值还可以理解为实际观察到的数据与原假设之间不一致程度的概率。p值越小，说明实际观测到的数据与原假设不一致的程度就越高，检验结果也就越显著。

p值是拒绝原假设的证据，是犯I类错误的实际概率。但是p值较小并不意味着效果一定大或重要，它只是表明数据与虚无假设不一致的程度。p值并不告诉我们虚无假设是错误的概率，也不直接告诉我们备选假设是正确的概率。

随着 p 值的减少，结论的可靠性越来越强，统计学根据显著性检验方法所得到的p 值，一般以 p< 0.05 为显著， p <0.01 为非常显著，在社会科学研究中，通常把 p≤0.05 作为显著水平的标准。但实际上，“显著”与“不显著”之间是没有清楚的界限的。

显著性水平α 和 p 值的关系在于，显著性水平 α 是研究者假定的理论值，而 p 值是利用样本计算得出的实际值。显著性水平表示所需的证据量，而p值表示样本中存在的证据的强度。当 p 值小于或等于显著性水平时，样本证据的强度等于或超过否定原假设并得出效应存在的结论的证据标准。

接收域与拒绝域

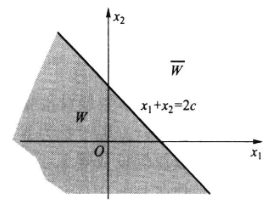
假设检验就是指这样的一个法则：当有了具体的样本后，按该法则就可决定是接受还是拒绝，即检验就等价于把样本空间划分成两个互不相交的部分\(W\)和\(\bar{W}\)。当样本属于\(W\)时，拒绝\(H_0\)，否则接受\(H_0\)．于是，我们称为\(W\)该检验的拒绝域，而称\(\bar{W}\)为接受域。

拒绝域示意图

选择拒绝域的核心思想就是：小概率事件不易发生。如果虚无假设正确的情况下发生了一个和虚无假设相违背的小概率事情，则可以认为虚无假设有误，所以拒绝虚无假设，否则就表示目前的样本数据还不能证明虚无假设不正确，可以暂时认为虚无假设正确。

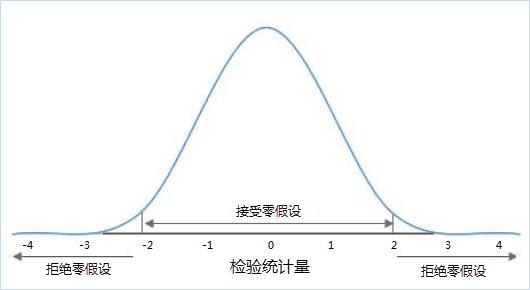
拒绝域在抽样分布内就是一段或两端的小区域，如果样本的统计值在此区域内，则否定虚无假设。

单侧检验与双侧检验

备选假设如果是以单向形式表述的，则对零假设的检验可为单侧检验。如果备选假设并没有清楚表达发生变化的方向，就要用双侧检验。

• 单侧检验：网课教学效果优于线下教学。
• 双侧检验：网课教学效果不同于线下教学。

一部分学者认为，如果对研究主题已有充分的了解或是预期的方向，应该采用单侧检验，但是也有相当的学者认为双侧检验比较不容易显著（因为临界值更大一些），因此如果双侧检验显著，就更有说服力。心理学研究的惯例是采用双侧检验。

假设检验的步骤

1. 建立假设：确定研究假设和虚无假设，根据研究假设选择单侧检验还是双侧检验；
2. 决定显著度水平（在社会科学中，\(α\) 一般取 0.05、0.01、0.001）；
3. 选定检验方法，计算检验统计量；
4. 计算出p值；
5. 根据计算结果和p值，作出决策（如果 \(p\) 值小于或等于 \(α\)，则否定虚无假设；反之则不否定虚无假设）。

在研究报告中，需要汇报研究假设、显著性水平和单侧检验或双侧检验。

非参数检验

含义

• 若假设可用一个参数的集合来表示，则该假设检验问题为参数假设检验问题，否则成为非参数假设检验问题。
• 非参数检验的着眼点不是总体的有关参数的比较，其推断方法和总体分布无法，而是分布位置、分布形状之间的比较，研究目标总体与理论总体的分布是否相同，或者各样本所在总体的分布位置是否相同等，不受总体分布的限定、适用范围广，故而称之为非参数检验。
• 非参数统计方法主要用于那些总体分布不能用有限个实参数刻画，或者不考虑被研究对象为何种分布以及分布是否已知的情形，它对总体分布几乎没有什么假定。

适用情形

1. 总体分布与参数检验所要求的的条件不符
2. 样本来自总体的分布未知
3. 变量为类别变量，不能计算均值
4. 数据虽为数值变量，但均值和方差无法计算
5. 数据不满足正态性、方差齐性等要求

非参数检验的缺点

检验效能较低。例如秩和检验的检验效能为t检验的90%-95%，其它非参数检验方法的效能更低。因此能使用参数检验方法，还是要首选参数检验。

性质

非参数检验法，不要求总体数值具备特殊的条件。但当样本量足够大时，非参数检验法的检验力也是很有保证的。

参考文献

1. 陈正昌, 贾俊平. (2016). 统计分析与R. 中国人民大学出版社.
2. 贾俊平. (2021). 统计学——Python实现. 高等教育出版社.
3. 李沛良. (2001). 社会研究的统计应用. 社会科学文献出版社.
4. 张文彤. (2017). SPSS统计分析基础教程（第3版）. 高等教育出版社.
5. Gudmund R. Iversen, M. G. (2002). 统计学：基本概念和方法 (吴喜之, 程博, 柳林旭, 仝莉萍, 钟文瑄, & 熊怀羽, 译). 高等教育出版社；施普林格出版社.
6. 柯惠新, & 沈浩. (2015). 调查研究中的统计分析方法‧基础篇. 中国传媒大学出版社.
7. statsmodels.stats.proportion.proportion_confint — statsmodels
8. Understanding Significance Levels in Statistics - Statistics By Jim