抽样
研究方法
抽样的意义
从样本中计算出来的数值,叫作统计值。对应的总体中的数值,则称为参数值。需要使用推论统计法用样本统计值去推测总体的参数值。
抽样的过程
- 界定总体;
- 搜集全部名单;
- 决定样本规模;
- 选取样本个案;
- 评估样本质量。
界定总体
总体的定义,越清楚越好。有样本所得的研究结果,原则上只能推论到这个所界定的总体范围。
搜集全部名单
根据总体的定义,收集一份全部个案的名单组成抽样框。
决定样本的大小
在决定样本大小时,应根据所能付出的研究代价的最大限度抽取最大的样本。
选取样本个案
设计抽样方案,从抽样框中选取所需的个案。
评估样本之正误
根据一些在总体与样本中都能容易找到的特征来评估样本的正误。
抽样分布
样本统计量的概率分布称为抽样分布(sampling distribution),它是由样本统计量的所有可能取值形成的相对频数分布。在使用统计量进行推论统计时常需要知道随机变量的分布。当总体的分布函数已知时,抽样分布是确定的。
根据统计量来推断总体参数具有某种不确定性,但我们可以给出这种推断的可靠性,度量这种可靠性的依据就是样本统计量的抽样分布。
抽样分布的作用
统计量的概率分布提供了该统计量长远且稳定的信息,它构成了推断总体参数值的理论基础。
常用抽样分布
二项分布
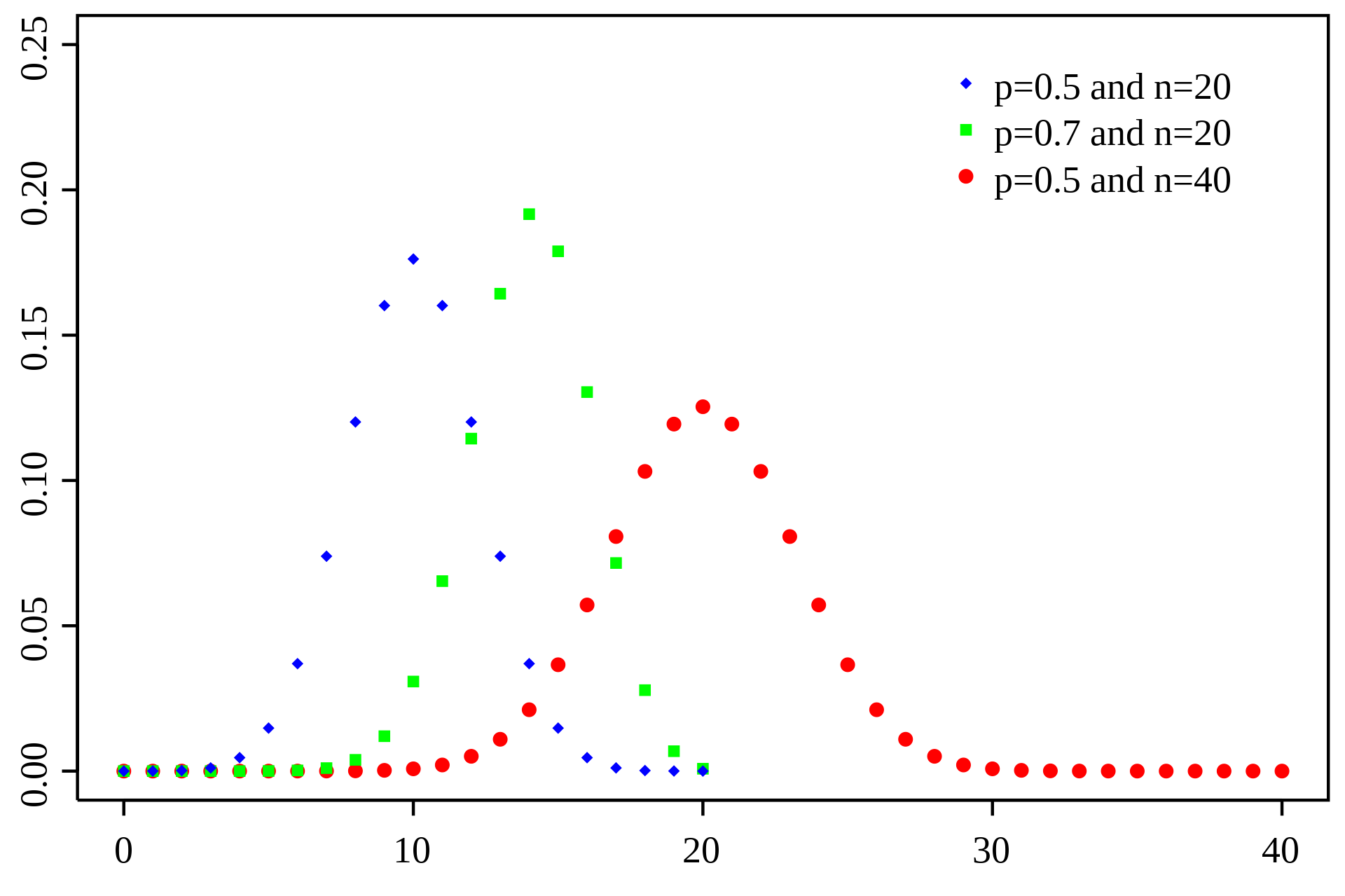
所谓二项,是指变量只有两个值。类别变量的值,可视为二项。在概率论和统计学里面,带有参数n和p的二项分布表示的是n次独立试验的成功次数的概率分布。在每次独立试验中只有取两个值,表示成功的值的概率为p,那么表示试验不成功的概率为1-p。这样一种判断成功和失败的二值试验又叫做伯努利试验。特殊地,当n=1的时候,我们把二项分布称为伯努利分布。
计算公式:
\[ p(r)=\dfrac{n!}{r!(n-r)!}P^rQ^{n-r} \]
- n:样本规模
- r:成功的数目
- P:每次的成功机会
- Q:每次的失败机会
- p(r):获得r次成功个案的概率
如果n=3,则在三个个案中有一次成功的概率为:
\[ p(1)=\dfrac{3!}{1!(3-1)!}0.5^10.5^{3-1}=\frac{3}{8} \]
二项分布的特点
- 当样本规模很大时,二项抽样分布(P=Q)可以近似为正态分布。当P不等于Q时(P+Q=1),抽样分布是不对称的,但是依然可以计算具体情况出现的概率。
- 随着抽样次数k的增加,概率先随之增加,到达最大值后单调减少。
其中卡方分布、t分布及F分布成为来自正态总体的三大抽样分布。
抽样方法
样本规模
抽样误差
参考文献
- 陈正昌, 贾俊平. (2016). 统计分析与R. 中国人民大学出版社.
- 贾俊平. (2021). 统计学——Python实现. 高等教育出版社.
- 李沛良. (2001). 社会研究的统计应用. 社会科学文献出版社.
- 张文彤. (2017). SPSS统计分析基础教程(第3版). 高等教育出版社.